|
From
http://www.johnsboatstuff.com/Articles/estimati.htm which has gone missing
from the web.
Those of us that sail small boats quickly develop an
appreciation for stability. All it takes is a gust of wind or a large wave, and
weíre wet. Larger boats, especially those designed for cruising, respond much
slower and usually give the impression of having a great deal of stability.
Under normal conditions virtually all large boats do have adequate stability,
but will this be true in a sever storm? Will they roll violently, or if knocked
down, will they come back upright? Whether going for a day sail or leaving on a
world cruise, Itís important that you answer these questions and understand the
key factors that determine stability.
Stability is the resistance of a boat to forces that tend to induce
heeling. These forces are usually static, like wind pressure on the sails, but
storm conditions can bring dynamic forces (wind gusts and breaking waves) into
play. Evaluating the overall stability of a blue water cruising boat requires
the consideration of both static and dynamic stability issues. Four key factors
are involved:
- Center of Gravity (known as ballast stability)
- Center of Buoyancy (form stability)
- Displacement (effects static and dynamic stability)
- Moment of Inertia (dynamic stability)
The first three factors determine static stability.
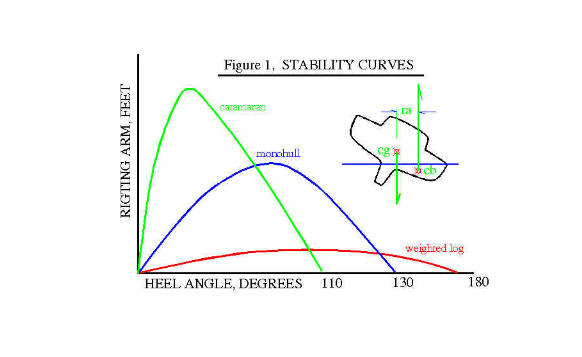
This is usually shown as a plot of "Righting Arm" VS "Heel Angle", as is shown
in Figure 1. The length of the righting arm is the horizontal distance between
the buoyant force and the center of gravity. The "Restoring Moment", which
represents stability, is simply the product of the righting arm and the
displacement. The righting arm begins at zero, increases to a maximum at around
40 degrees of heel, and then decreases until it reaches zero again around 130
degrees. The heel angle where the righting arm goes back to zero is referred to
as the "Angle of Positive Stability". When that angle is exceeded, the boat
capsizes.
Its popular to associate a large angle of positive
stability with "good stability", but by itself, it is not a good indicator
of stability. As an example, a log with a small weight nailed to one side
will have a very large angle of positive stability (almost 180 degrees), but
it will offer very little resistance to heeling. A boat built like this,
with a round bottom and very little ballast, would be dangerous, since it
would roll over a wide angle and could carry little sail. Catamarans are at
the other end of the scale, extremely stable at small heel angles, but only
a limited angle of positive stability. The area under the static stability
plot, which is a measure of how much energy is required to capsize the boat,
is more important than the angle of positive stability, and is a better way
to look at these plots. Since the actual restoring moment is the product of
the righting arm and displacement, heavy boats are inherently more stable
than light ones, all else being equal.
CG controlled stability is fairly straightforward. A heavy boat,
with a low center of gravity, will normally exhibit high stability. CB
controlled stability (often called form stability) is determined by the
center of buoyancy and its relationship to heel angle. In general, the wider
the boat, the more form stability, but at extreme heel angles, freeboard,
deck camber, and cabin dimensions all effect form stability.
Dynamic stability controls how much a boat heels in response to a
wind gust or impact of a strong wave. A stable cruising boat will resist
these dynamic forces long enough for them to pass safely by. Heavy
displacement helps dynamic stability, but the most important factor is the
boatís roll moment of inertia. The roll moment of inertia is calculated by
multiplying the weight of each piece of the boat by the square of its
distance from the center of gravity. The "squared" term makes the
calculation very sensitive to how far heavy objects are from the center of
gravity. For example, a dingy with two people sitting fore and aft on the
centerline has a smaller roll moment of inertia than the same dingy with the
people sitting side by side. Both boats weight the same, have the same
center of gravity, and the same center of buoyancy (exactly the same static
stability), but moving the people off the centerline greatly increases the
roll moment of inertia. If two identical boats are hit by a gust, the one
with the largest roll moment of inertia will roll the least. Deep draft,
heavy displacement hulls, with long heavy masts will have the largest roll
moment of inertia.
Boat designers rarely provide enough details for us to quantify
stability. Prospective buyers typically depend on advice from various
"experts", magazine reviews, or antidotal evidence from other sailors. While
these sources should not be ignored, its possible to "reverse engineer"
existing designs using only basic dimensions, like length overall (loa),
beam, displacement, draft, and ballast, and determine their relative
stability, compared to a standard. The key to this process is to generate a
standard, or "template", which is based on the characteristics of designs
known to have excellent stability. If our test boat fits inside this
template, we can assume its basic design is reasonable and similar to the
boats making up the template.
The credibility of the template must be extremely high for this
process to work. My approach was to base the template on the actual designs
of respected and proven cruising boat designers. Few will challenge the
quality of the designs by Carl Alberg, John Alden, Bill Crealock, Ted
Brewer, Lyle Hess, Ted Hood, Al Mason, Chuck Paine, and Robert Perry. I
collected data on 118 boats from these nine designers, and analyzed them
with respect to the following six basic non dimensional parameters:
Disp. / LWL
Sail Area / Disp.
LOA / Beam
Capsize Risk
Comfort Factor
Vmax / Vhull
I then used a "fuzzy logic" technique to identify boats that were
fully compatible with these parameters, drawing from my database, which
contains over 840 monohull sailboats. Fuzzy logic allows these boats to be
ranked with respect to how closely they match a "template" built with
parameters obtained from our selected cruising boat designers. The boats
that made it on this list are all "very close" to all of the parameters
derived from the work of our nine designers. The highest scoring designs
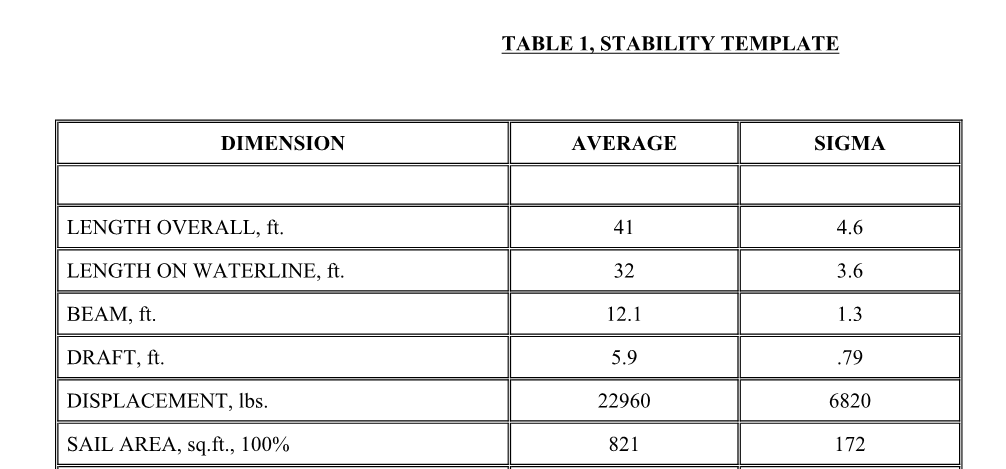
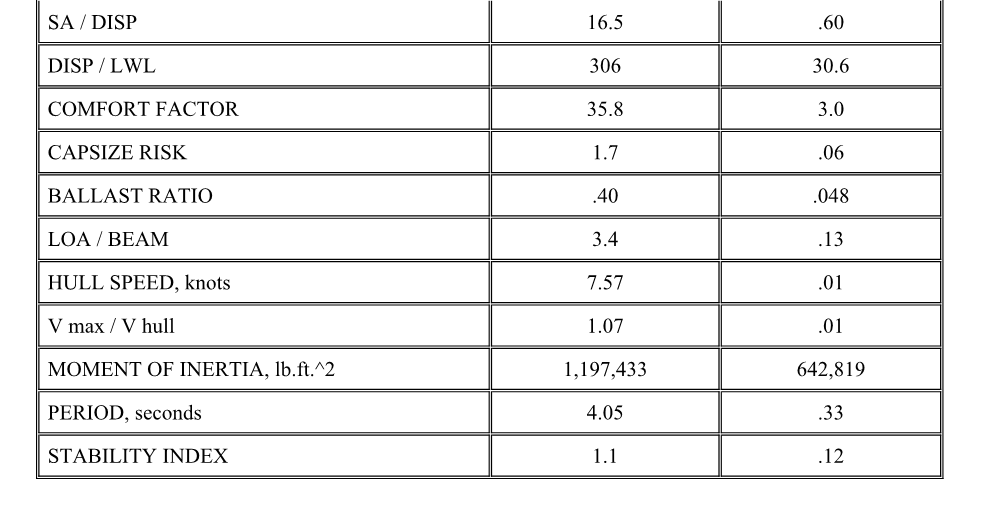
(above the 50 percentile), 55 total, were then selected for constructing the
template. Their average dimensions and standard deviations (sigma) are shown
in Table 1.
With our template in place, we can begin to see what type of boat our
designers favor for offshore cruising. Clearly these are not high performance
racers. They are large, heavy boats with high static and dynamic stability,
which will produce an easy ride with minimal crew fatigue. The calculated
template terms are discussed in the following section.
DISP / LENGTH RATIO = disp/2240/(.01*lwl)^3
Probably the most used and best understood evaluation factor. Low numbers
(resulting from lightweight and long waterlines) are associated with high
performance. The general trend for new boats is towards lower ratios that favor
higher performance. The trade off is that a light boat will have more violent
motion in storms. This requires constant attention to steering and sail trim,
resulting in crew fatigue. The ratio decreases with boat length, since heavy
boats need less ballast and will be lighter than smaller boats with the same
stability. Our template shows acceptable values between 265 and 337.
SAIL AREA / DISP RATIO = sail area/(disp/64)^.666
This is basically a ratio of power to weight, calculated using a 100% jib.
Most monohull designs range between 16 and 18. Our template numbers are a
conservative 15.9 to 16.5. The ratio is independent of boat length
HULL SPEED = 1.34*lwl^.5 ,knots
Generally regarded as the highest practical velocity for a displacement boat
assuming a reasonable power input (2-3 hp per ton). As a boat's speed increases,
the wave it creates becomes longer, creating a trough that moves aft. At hull
speed, the trough will be as long as the waterline length, creating a "hole"
that the boat just fits. An enormous amount of power (50-100 hp / ton) is
required to "climb out" of this hole and transition to higher speeds (planing).
The template value is 7.6 knots.
VELOCITY RATIO = 1.88*lwl^.5*sail area^.333/disp^.25 /
(hull speed)
The numerator of the equation calculates potential maximum speed, using an
empirical relationship. Boats with a generous sailplan and light displacement
will have a velocity ratio greater than 1. Under powered or extra heavy boats
will be less than 1. The template value of 1.07 predicts good performance under
sail.
BALLAST / DISP RATIO = ball/disp
One indicator of stability, but the center of gravity, center of buoyancy Vs
heel angle, and total weight are needed for a complete picture. Values range
from a low of .25 to a maximum of .5. The template value of .4 indicates more
emphasis on gravity controlled stability rather than form stability.
LOA / BEAM RATIO = loa/beam
This ratio measures the fineness of the hull. Fine hulls, having ratios of 3.0 -
4.0 and higher, are long and slender which promotes easy motion, high speed (low
drag), and good balance when heeled. Many newer designs favor wider hulls which
have larger interior volume, sail flatter, and have high reaching and down wind
speed potential. One note of caution when making comparisons, longer boats tend
to be finer then short ones. Our template value is 3.4, which is fairly fine.
Fine hulls tend to be well balanced and have low inverted stability.
CAPSIZE RISK = beam/(disp/(.9*64))^.333
An empirical factor derived by the USYRU after an analysis of the 1979 FASTNET
Race. The study was funded by the Society of Navel Architects and Marine
Engineers (SNAME). They concluded that boats with values greater than 2 should
not compete in ocean races. Values less than 2 are "good". The formula penalizes
boats with a large beam for their high inverted stability, and light-weight
boats because of their violent response (low roll moment of inertia) to large
waves, which are both very important during violent storms. It does not indicate
or calculate static stability. Some modern coastal cruisers and many racing
designs have problems meeting this criteria. An interesting note, the study
concluded that static stability was relatively unimportant in predicting dynamic
capsize. Beam and weight were much more important factors. Wide boats give waves
a longer lever arm to initiate roll and light weight boats require less energy
to roll over; both undesirable attributes in a cruising boat. The template value
of 1.7 is very low.
COMFORT FACTOR = disp/(.65*(.7*lwl+.3*loa)*beam^1.33)
An empirical term developed by yacht designer Ted Brewer. Large numbers indicate
a smoother, more comfortable motion in a sea-way. The equation favors heavy
boats with some overhang and a narrow beam. These are all factors that slow down
the boat's response in violent waves. This design philosophy is contrary to many
modern "racer / cruisers", but it is based on a great deal of real blue water
data, not just what looks good in a boat show. A value of 30 - 40 would be an
average cruiser. Racing designs can be less than 20, and a full keel, Colin
Archer design, could be as high as 60. Our template value of 36 indicates that
comfort is a high priority on cruisers.
MOMENT OF INERTIA (I) = disp^1.744/35.5
An empirical term developed by SNAME. Large values resist rolling forces. The
moment of inertia is very sensitive to the distance items are from the CG. A
heavy rig can greatly increase I, with little impact on displacement.
ROLL PERIOD (T) = 2*PI*(I/(82.43*lwl*(.82*beam)^3))^.5
The roll period is based on the moment of inertia. The term ".82*beam" has been
substituted for the waterline beam due to lack of data. Using ".82" results in a
close match for the few boats with measured periods, but more data is needed (If
you have measured roll data, email it to me and Iíll include it in my data
base). Simply stated, a sailboatís roll period, in seconds, is inversely
proportional to its stability. Unstable boats have long periods, stable boats
have short periods. The roll period is very easy to determine, you simply grab a
shroud and push / pull until the boat is rocking over a few degrees. Then count
the number of full cycles in one minute, and divide into 60. The general rule of
thumb is that boats with periods less than 4 seconds are stiff and periods
greater than 8 seconds are tender. The template value of 4.05 is near the stiff
end of the range, indicating good static stability.
STABILITY INDEX = T / (beam*.3048)
This is another empirical term relating period and beam to stability. Values
less than 1.0 are considered stiff. Values greater than 1.5 are considered
tender. I like this technique because its simple, and includes the hull form,
the center of gravity, and the roll moment of inertia, all in one easy to use
package. The template boat again leans towards the stiff side, with a value of
1.1.
In summary, all cruising boats use a combination of CG control, form
stability, and displacement to determine static stability. This value is then
used to size the sail area so that a generous amount of capsize resistance
exists under full sail and moderate wind conditions. This is a delicate part of
a boat design. Too much sail area will require early reefing or high heel
angles, to little and the boat will be a slug in light air. Dynamic stability is
also important and closely related to the moment of inertia. A high moment of
inertia helps survival in heavy weather. The roll period of a boat blends
elements of static and dynamic stability and can be useful when comparing
potential cruising boats.
While many other factors must go into selecting your ideal cruising
boat, following the basic Stability Template is a good first step. The designs
from these nine world class cruising boat designers have logged a great many sea
miles. If your boat is similar, you can have confidence that it has at least
some of the right stuff with regard to static and dynamic stability.
|